Need to calculate angles to cut capstone for a circle
lonestarmojo
11 years ago
Related Stories

GREEN BUILDINGHouzz Tour: Off-the-Grid Island Home Circles a Sunny Courtyard
A circular home is a cozy spot for gardening, woodworking and plenty of reading
Full Story
COMMUNITYNeighborhood Walkability: Get the Score
Hoofing it around is way easier when everything is near your house — and one tool tells you how walkable an area is before you move
Full Story
PAINTING10 Rules for Your Next Painting Project
Take your next painting journey from ‘argh!’ to ‘ta-da!’ with these designer tricks
Full Story
REMODELING GUIDESTransition Time: How to Connect Tile and Hardwood Floors
Plan ahead to prevent unsightly or unsafe transitions between floor surfaces. Here's what you need to know
Full Story
MORE ROOMS5 Ways to Decorate Around a Flat-Screen TV
Color, Placement and Accessories Help that Big Black Screen Blend In
Full Story
LIGHTING10 Ways to Get Your Lighting Right
Learn how to layer table lamps, floor lamps and overhead fixtures to get the lighting you need and the mood you want
Full Story
GREEN BUILDINGHow to Harvest Rainwater for Your Garden
Conserve a vital resource and save money by collecting stormwater for irrigation in a barrel or tank
Full Story
BATHROOM DESIGNDream Spaces: Spa-Worthy Showers to Refresh the Senses
In these fantasy baths, open designs let in natural light and views, and intriguing materials create drama
Full Story
LANDSCAPE DESIGNGarden Walls: Dry-Stacked Stone Walls Keep Their Place in the Garden
See an ancient building technique that’s held stone walls together without mortar for centuries
Full Story
SHOP HOUZZHouzz Products: Schoolhouse Design Rocks!
Score high in style with designs that are too cool for school
Full Story





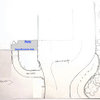



designoline6
Yardvaark
Related Professionals
Arlington Landscape Architects & Landscape Designers · Fort Lee Landscape Architects & Landscape Designers · Kapaa Landscape Architects & Landscape Designers · Manhattan Beach Landscape Architects & Landscape Designers · Norwood Landscape Contractors · Columbine Landscape Contractors · Dixon Landscape Contractors · Lexington Landscape Contractors · Newnan Landscape Contractors · River Ridge Landscape Contractors · Selden Landscape Contractors · Ankeny Decks, Patios & Outdoor Enclosures · Bellingham Decks, Patios & Outdoor Enclosures · Salisbury Decks, Patios & Outdoor Enclosures · Dickinson Swimming Pool Buildersdesignoline6